이진 탐색 트리의 문제점
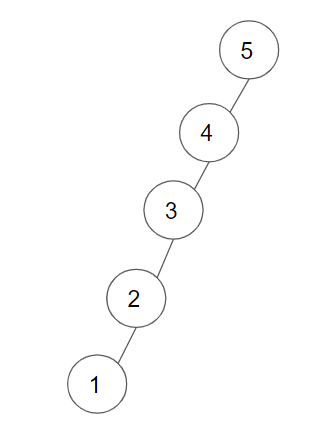
상위 노드를 기준으로 작으면 왼쪽, 크면 오른쪽으로 보내기 때문에 들어오는 순서에 따라 한 방향으로 치우칠 수 있다.
우리는 이것을 치우친 이진 트리(Skewed Binary Tree)라고 부른다.
AVL 트리란?
- 모든 리프 노드들의 레벨 차이는 1 이하
- 트리의 높이는 logN
- 삽입, 삭제, 탐색 연산에서 최악의 경우에도 O(logN)의 시간 복잡도를 보장한다.
Balance Factor
각 노드는 아래 공식으로 balance factor 수치를 계산해 트리의 균형 유무를 판단한다.
balance factor = 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이
- balance factor > 1: 왼쪽 서브 트리에서 불균형 발생
- balance factor < -1: 오른쪽 서브 트리에서 불균형 발생
이후에 나오는 그래프 그림에선 balance factor를 균형도라고 표현한다.
AVL 삽입
Rotation
삽입, 삭제 과정에서 트리의 균형을 맞추는 작업. 불균형이 발생한 노드를 기준으로 회전한다.
이후에 설명하겠지만, 2번 Rotation을 하는 상황은 왼쪽이나 오른쪽 자식 노드를 먼저 회전시킨다.
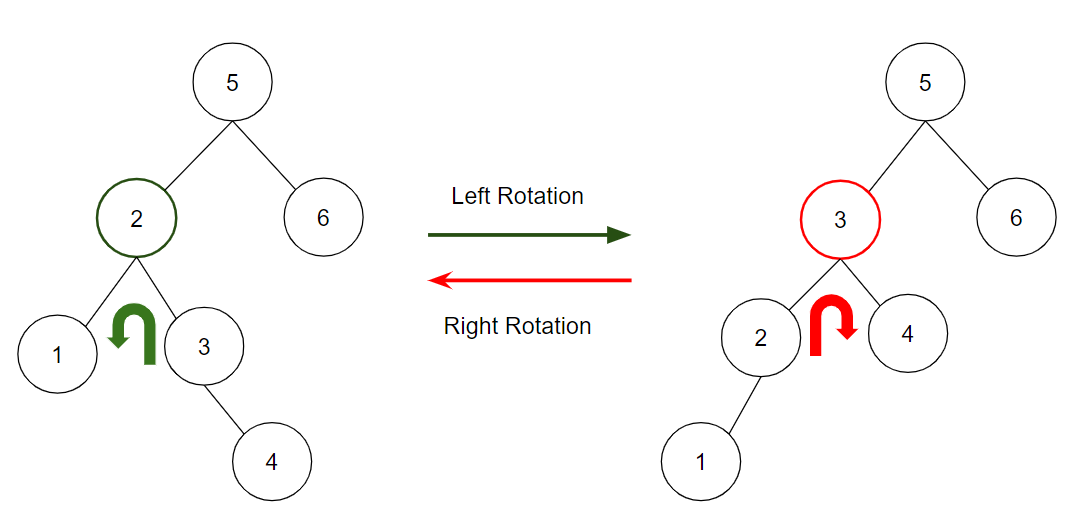
- Left Rotation: 기준 노드를 왼쪽으로 내리고 오른쪽 자식 노드를 위로 올린다.
- Right Rotation: 기준 노드를 오른쪽으로 내리고 왼쪽 자식 노드를 위로 올린다.
Roation은 순환 관계를 가진다.
회전을 한 뒤, 반대 방향으로 다시 Rotation을 하면 초기 상태로 돌아간다.
private static Node rightRotate(Node root) {
Node leftChild = root.left;
root.left = leftChild.right;
leftChild.right = root;
root.height = 1 + Math.max(getHeight(root.left), getHeight(root.right));
leftChild.height = 1 + Math.max(getHeight(leftChild.left), getHeight(leftChild.right));
return leftChild;
}
private static Node leftRotate(Node root) {
Node rightChild = root.right;
root.right = rightChild.left;
rightChild.left = root;
root.height = 1 + Math.max(getHeight(root.left), getHeight(root.right));
rightChild.height = 1 + Math.max(getHeight(rightChild.left), getHeight(rightChild.right));
return rightChild;
}Single Rotation
회전을 한 번만 시켜서 균형을 유지할 수 있는 상황을 말한다.
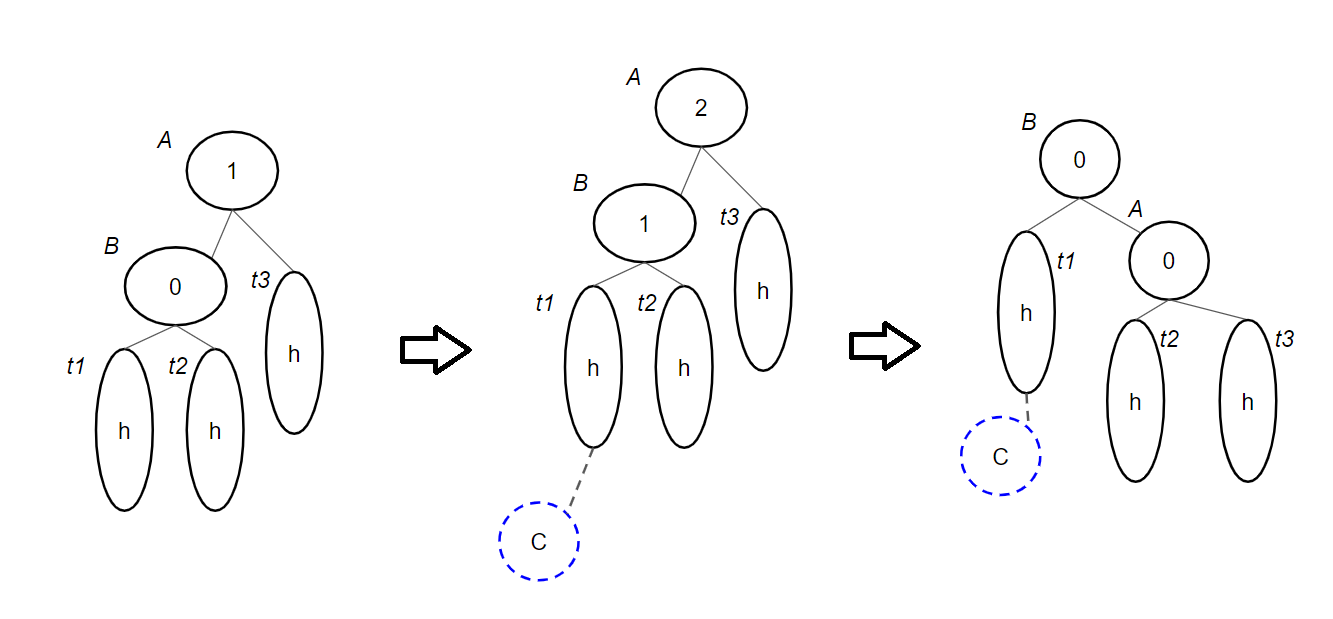
$A$: 루트 노드
$B$: $A$의 왼쪽 자식 노드
$t1$: $B$의 왼쪽 서브 트리
$t2$: $B$의 오른쪽 서브 트리
$t3$: $A$의 오른쪽 서브 트리
$t1$, $t2$, $t3$의 높이는 같다.
노드 안의 숫자는 balance factor이다.
현재 $A$의 balance factor는 $1$인 상태에서 새로운 노드 $C$가 $t1$의 왼쪽 노드에 추가되는 상황이다.
$t1$의 높이는 $h + 1$가 되면서 $B$의 balance factor는 0에서 1이 된고 높이는 $h + 2$가 된다.
이제 $A$의 balance factor는 $1$에서 $2$로 바뀌면서 좌측 서브 트리에 불균형이 발생한다. ($B$의 높이 - $t3$의 높이)
새로운 노드 $C$의 값이 노드 $B$보다 작기 때문에 트리는 왼쪽으로 치우친 상황이다.
이를 해결하기 위해 좌측 서브 트리를 위로 올려 오른쪽 서브 트리로 내려야 한다.
불균형이 감지된 노드를 기준으로 회전이 발생한다.
Single Rotation이 발생하는 경우는 2가지가 있다.
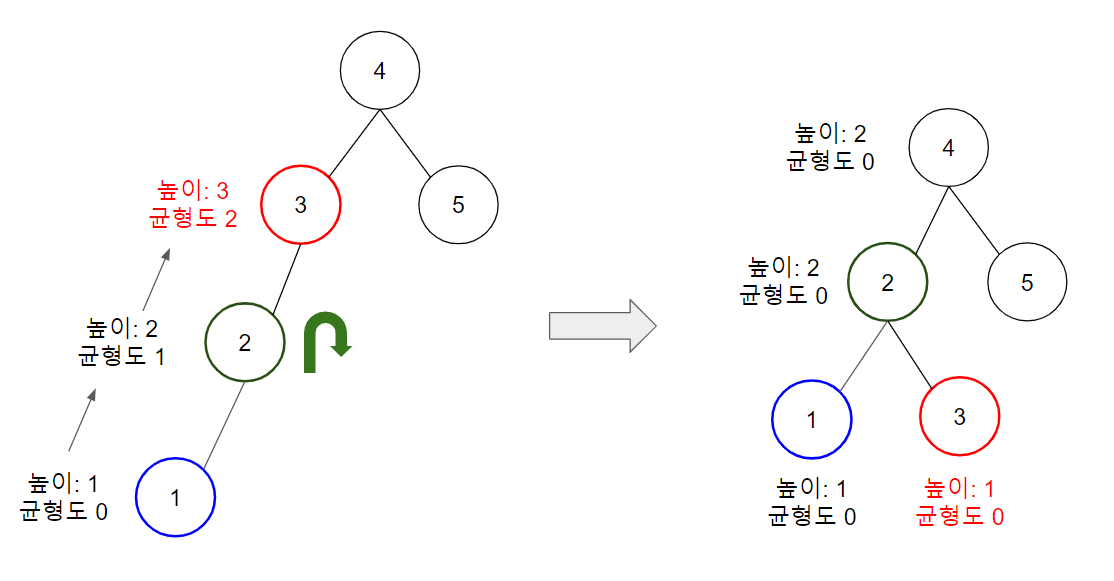
- Left - Left: $B$가 $A$의 왼쪽 자식 노드이고, 새로 삽입된 값이 $B$보다 작을 때
트리의 균형이 왼쪽으로 치우친 상황이니 Right Rotation을 수행한다.
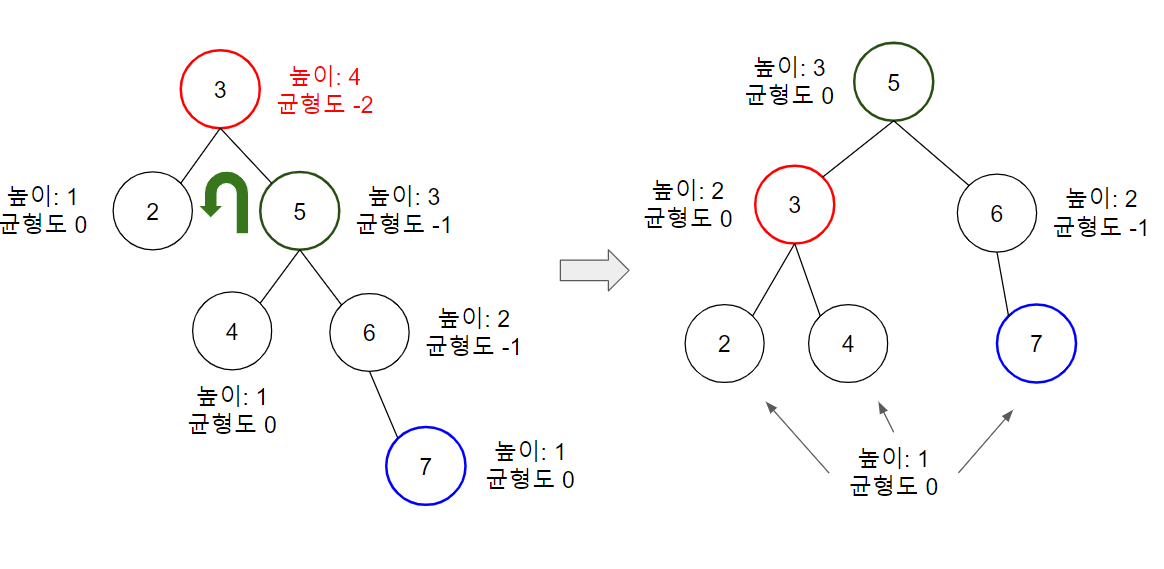
- Right - Right: $B$가 $A$의 오른쪽 자식 노드이고, 새로 삽입된 값이 $B$보다 클 때
트리의 균형이 오른쪽으로 치우친 상황이니 Left Rotation을 수행한다.
Double Rotation
Single Rotation을 수행해도 트리의 균형을 유지할 수 없는 상태. 이 경우, Rotation을 한 번 더 수행해야 한다.
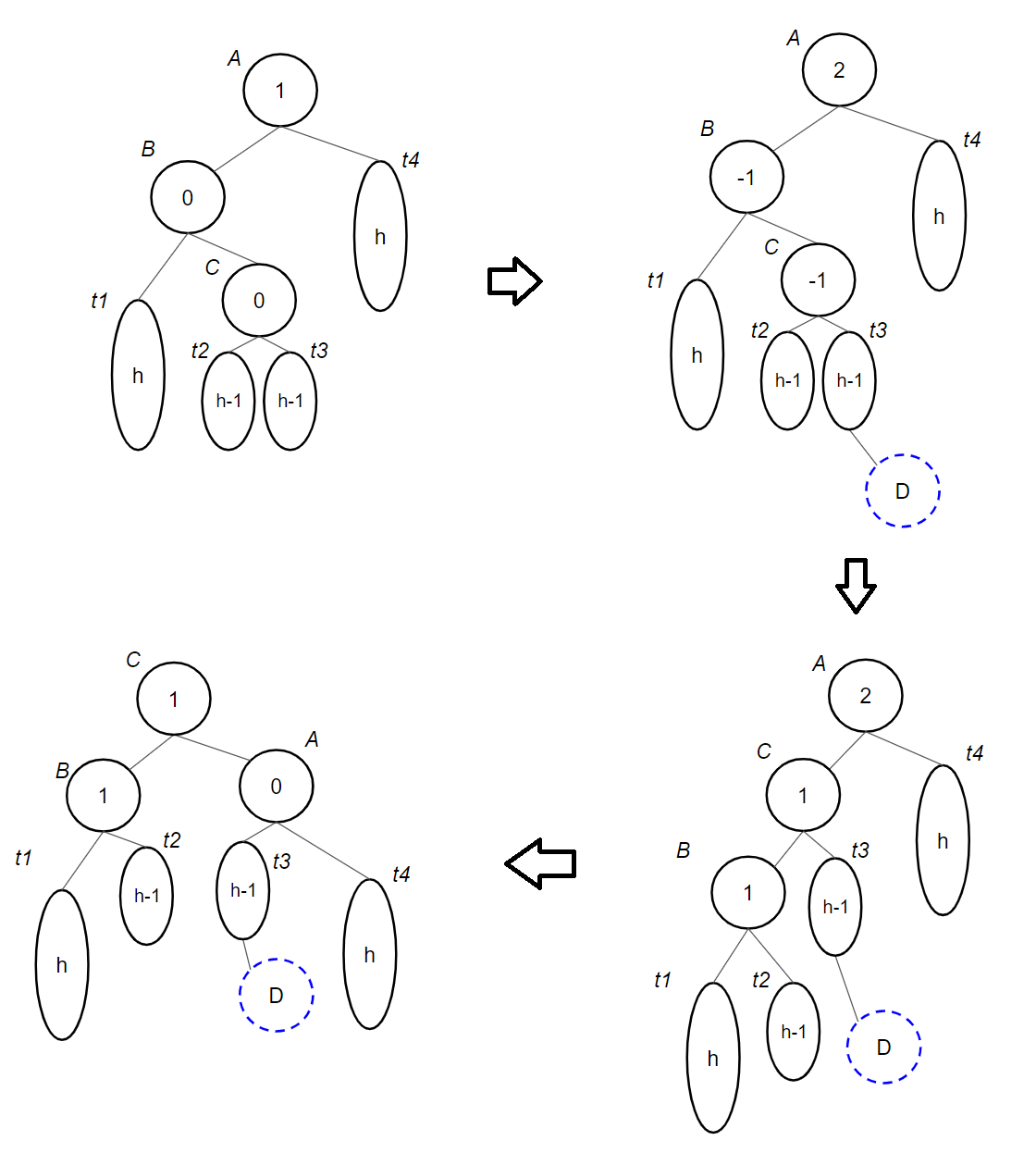
다음 그림에서 새로운 노드 $D$는 노드 $B$의 값보다 큰 상황이다.
노드 $A$의 왼쪽 자식 노드로 배치됐기 때문에 기존 Left-Left처럼 Right Rotaion을 해도 트리가 불균형이 된다.
이를 해결하기 위해, Single Rotation이 가능한 환경으로 만들어야 한다.
그림을 기준으로 $B$를 기준으로 Left Rotation을 수행해 Left-Left 상황으로 만든 뒤,
$A$를 기준으로 Right Rotation을 수행한다.
Double Rotation을 수행해야 하는 2가지 경우가 있다.
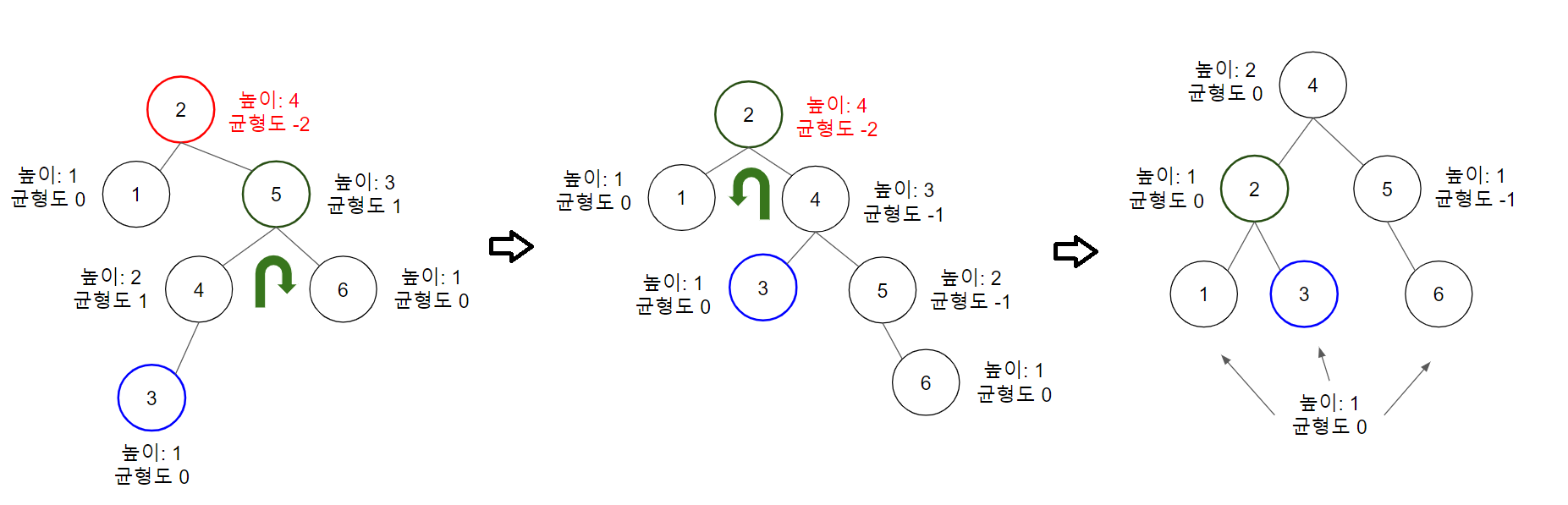
- Left-Right: $B$가 $A$의 왼쪽 자식 노드이고, 새로 삽입된 값이 $B$보다 클 때
Left Rotation을 통해 Left-Left 상황으로 맞춘 뒤, Right Rotaion을 수행한다.
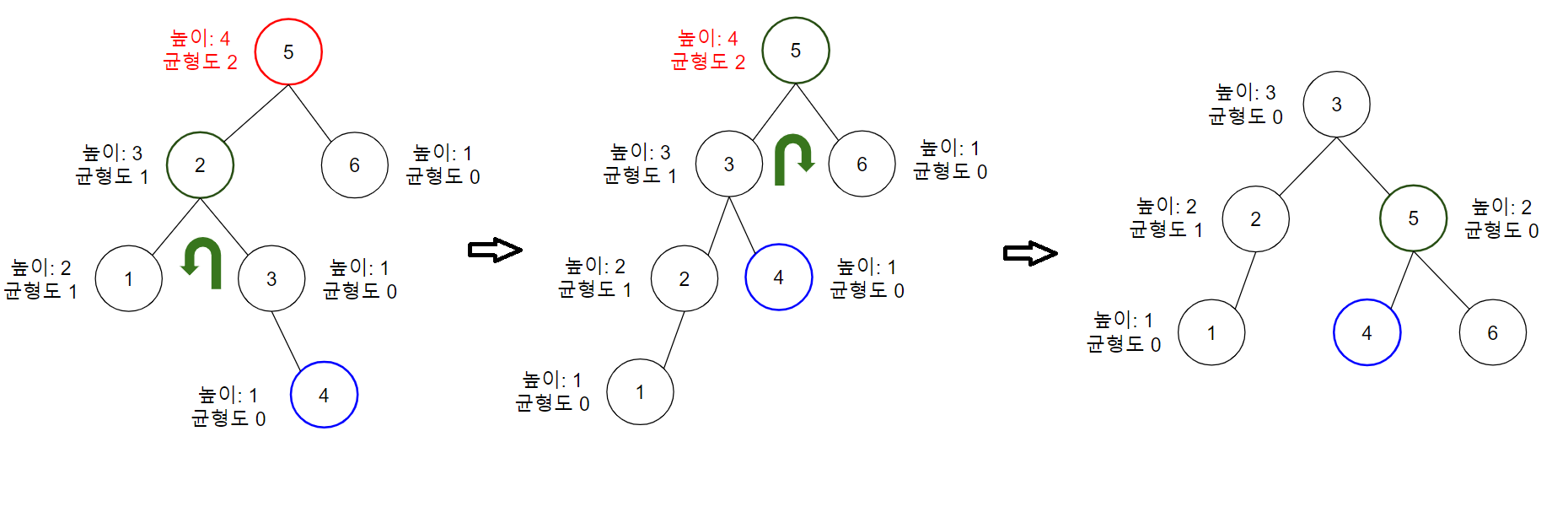
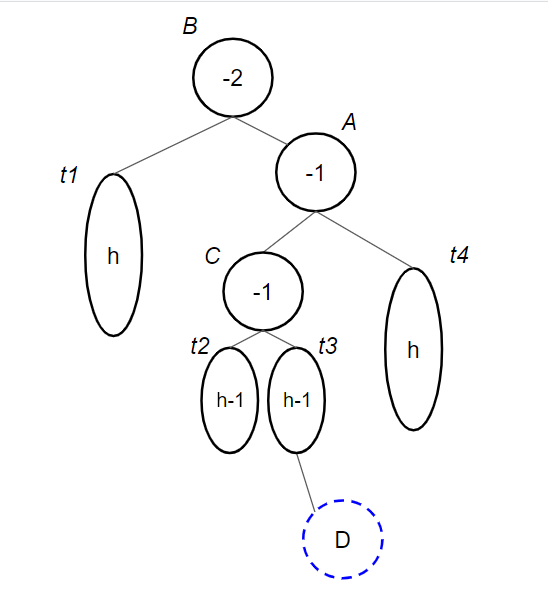
- Right-Left: $B$가 $A$의 오른쪽 자식 노드이고, 새로 삽입된 값이 $B$보다 작을 때
Right Rotation을 통해 Right-Right 상황으로 맞춘 뒤, Left Rotaion을 수행한다.
삽입에 대한 코드는 다음과 같다.
AVL 삭제
삭제 과정은 이진 탐색 트리와 동일하게 진행한다.
삭제할 노드를 발생한 시점부터 루트 노드로 올라가면서 높이와 balance factor를 갱신한다.
이 과정에서 불균형 트리가 감지된 경우 삽입 과정과 동일한 원리로 Signle 또는 Double Rotation을 수행한다.
그림으로 표현하기는 무척 복잡해 코드로 남긴다.
전체 코드
public class AVLTree {
private static class Node {
int key, height;
Node left, right;
public Node(int key) {
this.key = key;
this.height = 1;
this.left = null;
this.right = null;
}
}
private static Node root;
public static void main(String[] args) {
// testLeftLeftRotation();
// testLeftRightRotation();
// testRightRightRotation();
testRightLeftRotation();
}
private static Node insert(Node node, int key) {
if (node == null) {
return new Node(key);
}
if (node.key > key) {
node.left = insert(node.left, key);
}
if (node.key < key) {
node.right = insert(node.right, key);
}
// 트리의 불균형을 확인하는 단계
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
int balanceFactor = calcBalanceFactor(node);
// 왼쪽 서브트리 높이가 더 큰 경우 왼쪽 서브 노드를 위로 올려야 한다.
if (balanceFactor > 1) {
// Left-Left
if (node.left.key > key) {
return rightRotate(node);
}
// Left-Right
else if (node.left.key < key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
}
// 오른쪽 서브트리 높이가 더 큰 경우 오른쪽 서브 노드를 위로 올려야 한다.
else if (balanceFactor < -1) {
// Right-Left,
if (node.right.key > key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// Right-Right
else if (node.right.key < key) {
return leftRotate(node);
}
}
return node;
}
private static int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
private static int calcBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
private static Node rightRotate(Node root) {
Node leftChild = root.left;
root.left = leftChild.right;
leftChild.right = root;
root.height = 1 + Math.max(getHeight(root.left), getHeight(root.right));
leftChild.height = 1 + Math.max(getHeight(leftChild.left), getHeight(leftChild.right));
return leftChild;
}
private static Node leftRotate(Node root) {
Node rightChild = root.right;
root.right = rightChild.left;
rightChild.left = root;
root.height = 1 + Math.max(getHeight(root.left), getHeight(root.right));
rightChild.height = 1 + Math.max(getHeight(rightChild.left), getHeight(rightChild.right));
return rightChild;
}
private static Node delete(Node node, int key) {
if (node == null) {
return null;
}
// 탐색
if (node.key > key) {
node.left = delete(node.left, key);
} else if (node.key < key) {
node.right = delete(node.right, key);
} else {
// 삭제 과정
// 자식 노드가 없는 경우(리프 노드)
if (node.left == null && node.right == null) {
node = null;
return null;
}
// 자식 노드가 2개일 때
else if (node.left != null && node.right != null) {
Node predecessor = findPredecessor(node.left);
node.key = predecessor.key;
node.left = delete(node.left, predecessor.key);
}
// 자식 노드가 1개일 때
else {
if (node.left != null) {
node = node.left;
}
if (node.right != null) {
node = node.right;
}
return node;
}
// 높이 갱신
if (node == null) {
return null;
}
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
int balanceFactor = calcBalanceFactor(node);
// 왼쪽 서브트리 높이가 더 큰 경우 왼쪽 서브 노드를 위로 올려야 한다.
if (balanceFactor > 1) {
// Left-Left
if (node.left.key > key) {
return rightRotate(node);
}
// Left-Right
else if (node.left.key < key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
}
// 오른쪽 서브트리 높이가 더 큰 경우 오른쪽 서브 노드를 위로 올려야 한다.
else if (balanceFactor < -1) {
// Right-Left,
if (node.right.key > key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// Right-Right
else if (node.right.key < key) {
return leftRotate(node);
}
}
}
return node;
}
private static Node findPredecessor(Node node) {
if (node.right != null) {
return findPredecessor(node.right);
}
return node;
}
private static void preOrder(Node node) {
if (node == null) {
return;
}
System.out.printf("%d ", node.key);
preOrder(node.left);
preOrder(node.right);
}
private static void testLeftLeftRotation() {
System.out.println("-----LeftLeftRotation-------");
root = null;
root = insert(root, 4);
root = insert(root, 3);
root = insert(root, 5);
root = insert(root, 2);
preOrder(root);
root = insert(root, 1);
System.out.println();
preOrder(root);
}
private static void testLeftRightRotation() {
System.out.println("\n-----LeftRightRotation------");
root = null;
root = insert(root, 5);
root = insert(root, 2);
root = insert(root, 6);
root = insert(root, 1);
root = insert(root, 3);
preOrder(root);
root = insert(root, 4);
System.out.println();
preOrder(root);
}
private static void testRightRightRotation() {
System.out.println("\n----RightRightRotation------");
root = null;
root = insert(root, 3);
root = insert(root, 2);
root = insert(root, 5);
root = insert(root, 4);
root = insert(root, 6);
preOrder(root);
root = insert(root, 7);
System.out.println();
preOrder(root);
}
private static void testRightLeftRotation() {
System.out.println("\n-----RightLeftRotation------");
root = null;
root = insert(root, 2);
root = insert(root, 1);
root = insert(root, 5);
root = insert(root, 4);
root = insert(root, 6);
preOrder(root);
root = insert(root, 3);
System.out.println();
preOrder(root);
}
}https://github.com/brorica/DataStructure/blob/master/src/AVLTree.java
GitHub - brorica/DataStructure: 수상할 정도로 나무를 좋아하는 레포
수상할 정도로 나무를 좋아하는 레포. Contribute to brorica/DataStructure development by creating an account on GitHub.
github.com
'알고리즘' 카테고리의 다른 글
| 레드 블랙 트리(red black tree) (0) | 2023.06.25 |
|---|---|
| 이진 힙(binary heap) (1) | 2023.06.14 |
| 이진 탐색 트리 (Binary Search Tree) (0) | 2023.06.10 |
| 트리, 이진트리 (1) | 2023.06.09 |
| 2022 KAUPC 2회 출제 후기 (0) | 2022.09.18 |



