각 개체들의 집합 상태를 트리로 표현한 하나의 자료 구조다.
도식화한 모습이 트리 형태란 거지, 실제로 트리 자료구조를 직접 구현해야 하는 것은 아니다.
정확히는 각 개체들끼리 공통 부분이 없어야 한다는 조건이 있지만,
이 설명은 서로소란 것에 대한 수학적 접근이 필요하므로 위키를 보는 것을 추천한다.
+
대부분 블로그 설명을 보면 정점끼리 묶는 예시가 많고 이 블로그도 그렇게 작성했다.
다만, 어떤 경우에는 정점이 아닌 다른 부분들을 합쳐야 한다는 것을 알아두자.
ex) 간선의 가중치 등
다음과 같이 1~5 까지의 노드가 있다.
처음 각 노드들의 root 노드는 자기 자신이다. (부모 노드라 하는게 맞는데 편의상 root로 함)

Union
서로 다른 두 개체를 합친다.
정확히는 값이 낮은 개체로 union된다.
개체 1과 2를 합친 결과는 다음과 같다.
1이 2보다 작기 때문에, 1이 root 노드가 된다.

그 다음 3, 4, 5를 합치는 경우의 수 중 하나는 다음과 같다.
형태나 테이블 값은 다르더라도, 모든 경우에서 3이 root 노드가 된다.

이제 이 두 집합을 union한 결과는 다음과 같다.
결과를 보면 노드 4, 5의 root 노드가 1이 아닌 3으로 나와 있다.
이 부분에 대해선 find 파트에서 자세히 다룬다.

지금 까지 진행한 코드는 다음과 같다.
전체 코드는 맨 밑에 접어놨다.

Find
현재 노드의 root 노드를 찾는다.
위의 트리 형태에서 노드 5의 root 노드를 찾는 과정은 다음과 같다.
1. node 5의 root 노드인 3으로 이동
2. node 3의 root 노드인 1로 이동.
3. node 1의 root 노드는 1 자기 자신이므로, 해당 노드의 값인 1 return.

여기서 return을 한다는 것이 중요하다.
노드의 개수가 많아지다 보면, 트리의 depth가 길어지는 상황이 발생한다.
이런 상황에서 매번 O(N) 만큼의 시간 복잡도가 발생하고
트리의 depth가 깊어질 수록 하위 노드에 대한 연산은 비싸진다.
다행이도 이 연산을 O(1) 시간에 끝내는 방법이 있다.
Find를 수행하면서 얻은 root 노드의 값을 아래로 내려보내야 한다.
따라서 Find 과정은 재귀로 구성되고, node 5에 대한 find가 진행된 최종 형태는 다음과 같다.

마찬가지로 4에 대한 find를 진행하면 다음과 같다.

Find에 대한 코드는 다음과 같다.

이 Find를 기반으로 구성된 Union은 다음과 같다.
각 노드를 무작정 합칠 수 없으니, 두 노드의 root 노드를 파악한다.
이 과정에서 거쳐가는 노드들의 root 노드도 갱신이 된다.
만약, u == v라면 두 노드는 같은 root 노드, 즉 연결된 상태이다.
u != v라면 두 노드는 서로 다른 집합이기 때문에, 값이 작은 노드에 병합해준다.
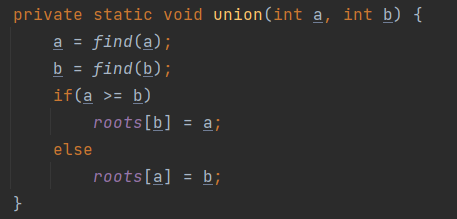
전체 코드는 아래 접어놨다.
public class Main {
static int[] nodes = new int[5];
public static void main(String[] args) {
// 처음 노드들은 자기 자신이 root 노드
for (int i = 0; i < 5; i++) {
nodes[i] = i + 1;
}
union(1, 2);
union(3, 4);
union(3, 5);
union(1, 5); // 역시 1대신 2를, 5대신 3, 4를 써도 된다.
}
private static void union(int u, int v) {
u = find(u);
v = find(v);
// 값이 작은 노드가 root 가된다.
if (u <= v)
nodes[v] = u;
else
nodes[u] = v;
}
private static int find(int node) {
if (nodes[node] == node)
return node;
return nodes[node] = find(nodes[node]);
}
}
+ Weighted Union
Union - Find 연산은 해당 집합 트리의 depth에 의해 속도가 결정 된다.
여기에 대한 최적화로 depth가 낮은 트리를 높은 트리에 union 하는 것이다.

위의 상황에서는 1을 root로 하는 트리의 depth가 작기 때문에
depth가 더 큰 3을 root로 하는 트리에 union된다.

하지만 이러면 depth 정보를 가진 배열을 하나 더 추가해야 돼서 메모리 사용이 증가한다.
이를 위한 방법으로 부모 노드는 양수, depth는 음수로 표현하는 방법이 있다.
처음 상태로 돌아가면 node 정보는 다음과 같다.
depth를 전부 -1로 설정한다.

노드 1, 2를 union을 한다면
노드 1, 2의 root 노드를 찾은 뒤, depth 큰 쪽에 union한다.
만약, depth 같다면 값이 작은 쪽에다 union 한다.

노드 3, 4를 union한 결과다.

이 노드 3과 노드 5를 union 하면 다음과 같이 된다.

이렇게 되면 find 연산이 조금 달라진다.
기존은 root가 자기 자신이면 find를 끝냈지만,
여기선 depth가 음수이면 해당 index를 반환한다.
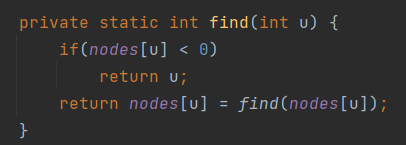
전체 코드는 접어놨다.
import java.util.Arrays;
public class Main {
static int[] nodes = new int[5];
public static void main(String[] args) {
Arrays.fill(nodes, -1);
union(1, 2);
union(3, 4);
union(3, 5);
union(1, 5); // 역시 1대신 2를, 5대신 3, 4를 써도 된다.
}
private static boolean union(int u, int v) {
u = find(u);
v = find(v);
if(u == v)
return true;
if(nodes[u] < nodes[v]) {
nodes[u] += nodes[v];
nodes[v] = u;
}
else {
nodes[v] += nodes[u];
nodes[u] = v;
}
return false;
}
private static int find(int u) {
if(nodes[u] < 0)
return u;
return nodes[u] = find(nodes[u]);
}
}'알고리즘 > 기법' 카테고리의 다른 글
| 위상 정렬(topological sorting) (0) | 2022.02.05 |
|---|---|
| 최소 스패닝 트리(MST, Minimum spanning tree) (0) | 2022.01.20 |
| BFS(breadth first search) (0) | 2022.01.17 |
| DFS(depth first search) (0) | 2022.01.15 |
| 0-1 BFS (0) | 2021.11.21 |


