그래프 순회 방법 중 하나
DFS가 깊이(depth)라면, BFS는 너비(breadth) 우선 탐색이기 때문에
정점에서 인접한 정점들을 우선 탐색한다.
주로 큐를 이용해 구현한다.
우선순위 큐로 구현한다면 다익스트라 알고리즘이 된다.
BFS 진행은 3단계로 나눌 수 있다.
1. 시작 index를 정한다.
2. 정점의 이동반경을 확인한다.
3. 방문하지 않은 정점이 있다면, 탐색 큐에 넣어준다.
BFS 탐색 순서는 다음과 같다.
시작 index는 1이라 가정한다.
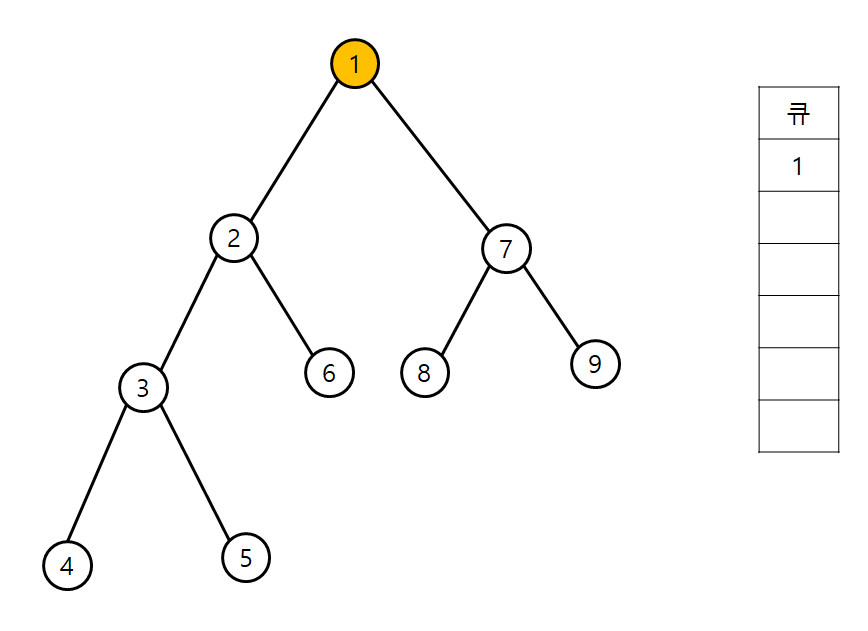
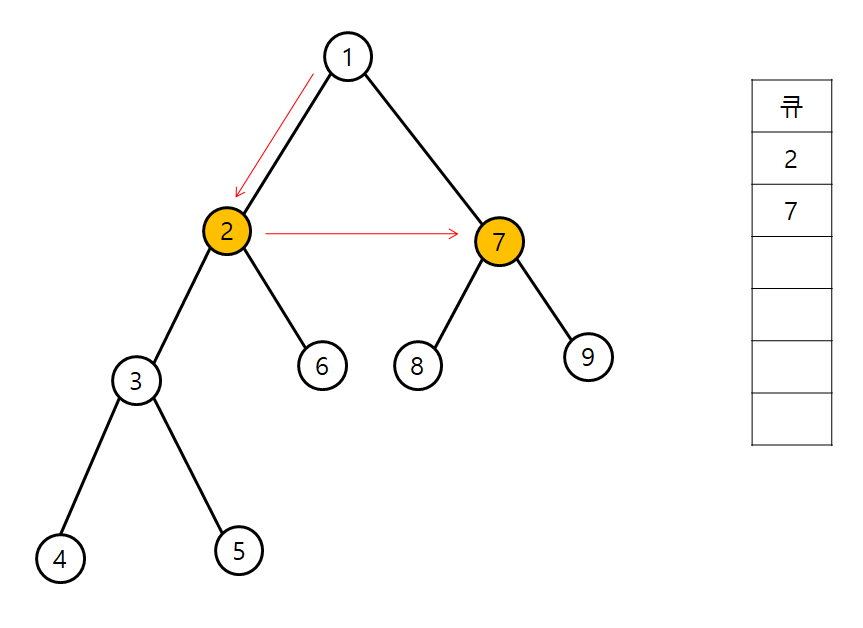
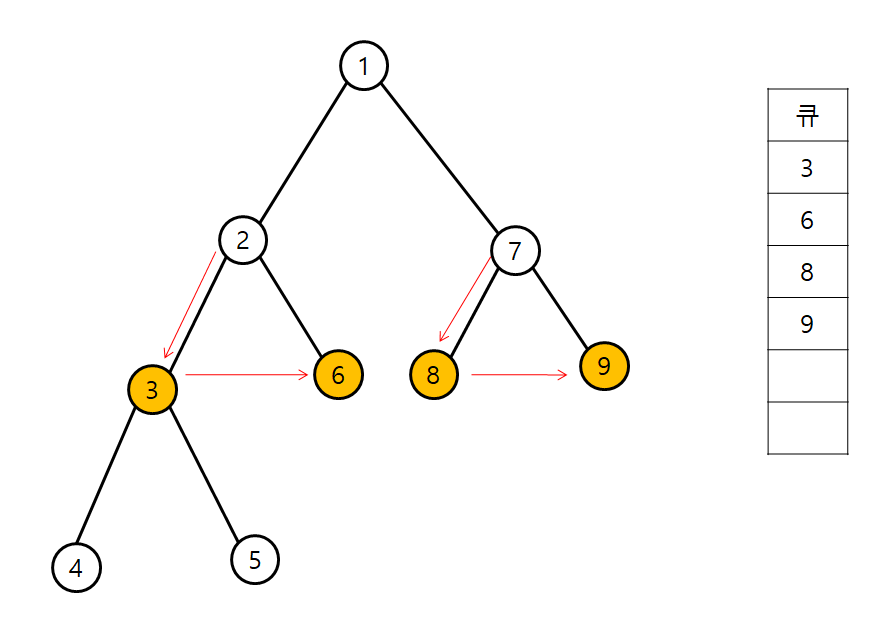
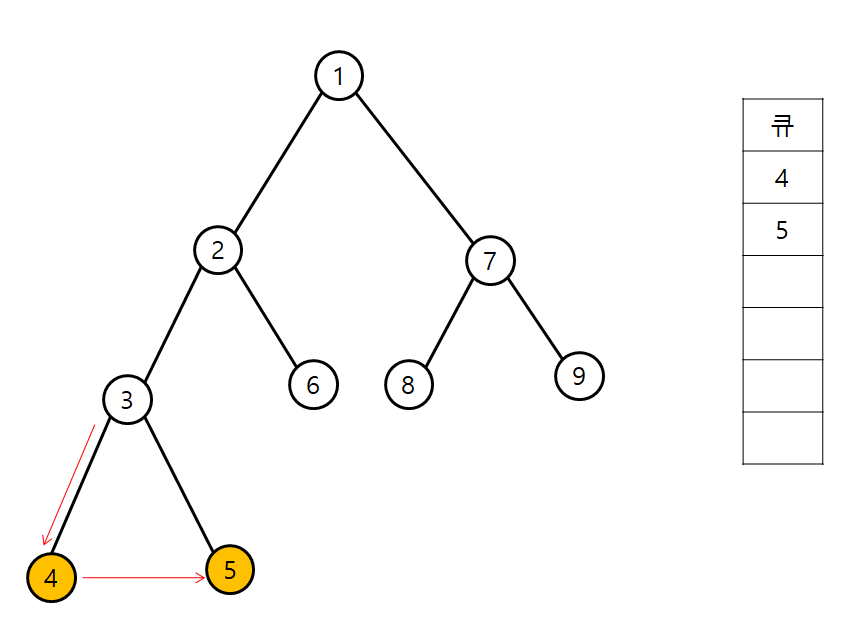
인접 리스트에서 BFS 코드
더보기
import java.io.*;
import java.util.*;
class Main {
static ArrayList<Integer>[] graph = new ArrayList[10];
public static void main(String[] args) throws Exception {
// 초기화
for (int i = 0; i < 10; i++) {
graph[i] = new ArrayList<>();
}
graph[1].add(2); graph[1].add(7);
graph[2].add(1); graph[2].add(3); graph[2].add(6);
graph[3].add(2); graph[3].add(4); graph[3].add(5);
graph[7].add(1); graph[7].add(8); graph[7].add(9);
BFS();
}
private static void BFS() {
boolean[] visit = new boolean[10];
Queue<Integer> q = new LinkedList<>();
q.add(1); // 1부터 탐색 시작
visit[1] = true;
while (!q.isEmpty()) {
int here = q.poll();
System.out.printf("%d ", here);
for(int index : graph[here]) {
if(visit[index])
continue;
visit[index] = true;
q.add(index);
}
}
}
}
인접 행렬에서의 BFS 코드
다음 배열을 상하좌우로 탐색한다고 가정한다.
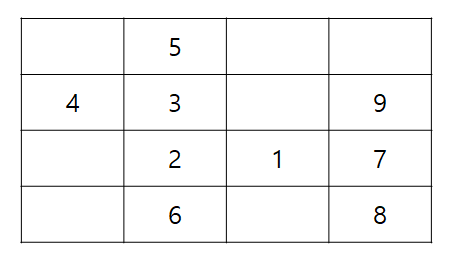
import java.io.*;
import java.util.*;
class Main {
static int[][] map = {
{0, 5, 0, 0},
{4, 3, 0, 9},
{0, 2, 1, 7},
{0, 6, 0, 8}};
static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 순서는 자유다.
public static void main(String[] args) throws Exception {
BFS();
}
private static void BFS() {
boolean[][] visit = new boolean[4][4];
Queue<Pair> q = new LinkedList<>();
q.add(new Pair(2, 2)); // 1부터 시작.
visit[2][2] = true;
int hereR, hereC, thereR, thereC;
while (!q.isEmpty()) {
Pair here = q.poll();
hereR = here.r;
hereC = here.c;
System.out.printf("%d %d\n", hereR, hereC);
for (int d = 0; d < 4; d++) {
thereR = hereR + dir[d][0];
thereC = hereC + dir[d][1];
// 배열 밖으로 나가는지 검사.
if(thereR < 0 || thereR >= 4 || thereC < 0 || thereC >= 4)
continue;
// 이미 방문한 적 있는 정점과 0은 탐색 큐에 넣지 않음
if (visit[thereC][thereR] || map[thereC][thereR] == 0)
continue;
// 탐색 큐에 넣음
visit[thereC][thereR] = true;
q.add(new Pair(thereR, thereC));
}
}
}
}
class Pair {
int r, c; // x, y
public Pair(int r, int c) {
this.r = r;
this.c = c;
}
}
시간 복잡도
정점이 V, 간선이 E일 때
인접 리스트 : O(V + E)
인접 행렬 : O(V * V)
BFS를 써야 할 때
개인적인 기준이다.
한 정점에 대한 연산에서 주변의 상황을 봐야 한다면 BFS를 쓴다.
ex) 값이 3인 정점이 있다면, 해당 정점과 인접한 정점에 3을 더해준다.
'알고리즘 > 기법' 카테고리의 다른 글
| 위상 정렬(topological sorting) (0) | 2022.02.05 |
|---|---|
| 최소 스패닝 트리(MST, Minimum spanning tree) (0) | 2022.01.20 |
| DFS(depth first search) (0) | 2022.01.15 |
| 유니온 파인드(Union Find) (0) | 2022.01.13 |
| 0-1 BFS (0) | 2021.11.21 |



