유향그래프에서 각 정점들이 한 방향으로 나열된 형태
정점 u와 v가 u -> v 순서일 때, 어떠한 경우에도 u -> v 순서가 유지된다.
이러한 특성 때문에 사이클이 존재하지 않는다.
주로 다음과 같은 곳에 사용된다.
1. 소프트웨어 공학에서 일정 계획 방법론인 PERT나 CPM
2. 스킬트리, 선수과목 같은 사전 작업같은 것이 필요한 작업들
물론, BFS/DFS만으로 풀 수 있지만
위상 정렬을 알면 더 쉽게 풀 수 있다.
위상 정렬의 수행 과정
2개 배열이 필요하다.
해당 정점에 연결된 간선의 수를 담는 배열 A
정점별로 간선 자료구조를 담는 배열
먼저, 자신을 가리키는 간선이 없는 정점들을 찾는다.
해당 정점에서 출발하는 간선이 있으면 지움 (배열 A의 카운트를 1 줄인다.)
만약, 해당 간선의 도착 정점이 더 이상 자신을 가리키는 간선이 없으면 탐색 큐에 추가.
(배열 A의 카운트가 0일 때)
다음 그래프가 있다고 할 때, 간선의 수를 담는 배열 A는 다음과 같다.

정점 1과 2는 자기로 향하는 간선이 없으므로, 여기서부터 탐색을 시작한다. (빨간색 원)
정점 1은 3과 이어진 간선을 지우고(회색 처리) 배열 A 카운트를 1깎는다.
이 때 정점 3의 배열 A 카운트는 0이 됐으므로 정점 3을 탐색 큐에 넣는다.
정점 2도 마찬가지로 정점 4와 이어진 간선을 지우고 배열 A 카운트를 1 깎는다.
이런식으로 진행한다.


이렇게 모든 정점 V와 모든 간선E을 한번씩 탐색하므로
시간 복잡도는 O(V + E)를 가진다.
코드는 접어놨다.
import java.util.*;
class Main {
static int N = 9;
static int[] count;
static ArrayList<Integer>[] graph;
public static void main(String[] args) {
init();
topologicalSorting();
}
private static void topologicalSorting() {
Queue<Integer> q = new LinkedList<>();
// 자신을 가리키는 간선이 없는 정점 탐색
for (int i = 1; i <= N; i++) {
if (count[i] == 0)
q.add(i);
}
int here;
while (!q.isEmpty()) {
here = q.poll();
for (int there : graph[here]) {
// 해당 간선 없는 걸로 처리
count[there]--;
// 만약 대상 정점을 가리키는 간선이 없다면
// 그 정점을 탐색 큐에 넣음
if (count[there] == 0) {
q.add(there);
}
}
}
}
private static void init() {
count = new int[N + 1];
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
graph[1].add(3);
graph[2].add(4);
graph[3].add(4); graph[3].add(5);
graph[4].add(8);
graph[5].add(6); graph[5].add(7);
graph[6].add(7);
graph[7].add(8);
}
}
위상정렬의 응용
만약, dp를 사용했다면 최적의 답과
그 답을 찾기 위해 지나온 경로를 추적할 수 있다.
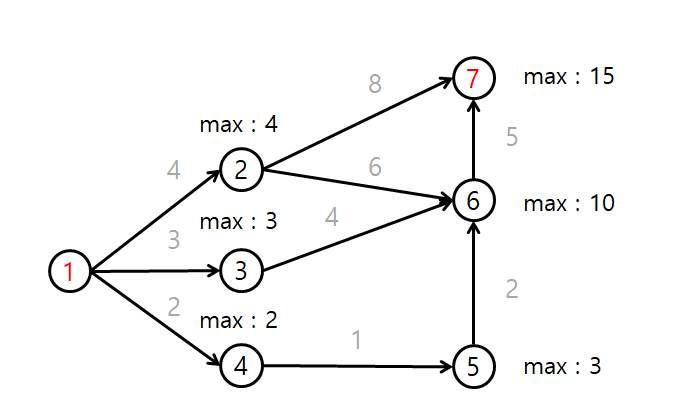
아래 그림처럼 간선에 가중치가 주어진 유향 그래프가 있고,
정점 1에서 정점 7까지 비용이 가장 크게 나오는 경로를 찾아야 하는 경우가 있다.
방법은 되게 간단한데, 간선의 방향을 전부 뒤집으면 된다.

먼저 각 정점들의 dp 값을 구하면 다음과 같다.
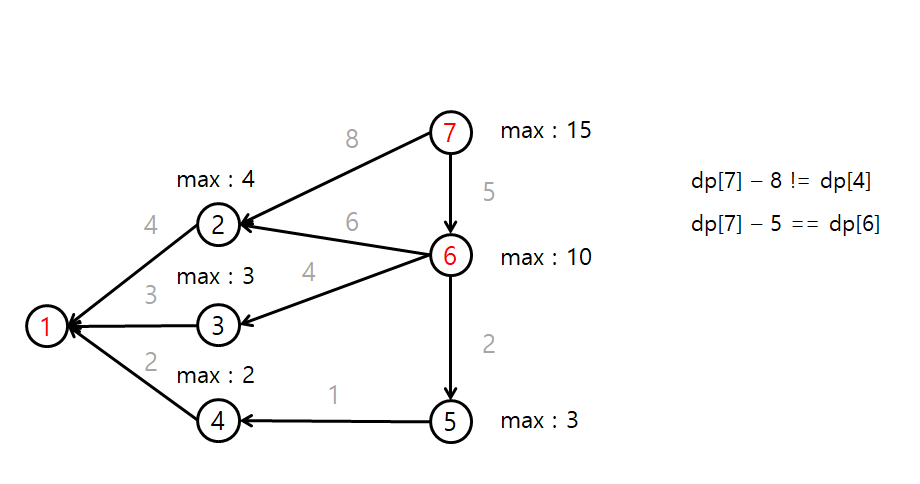
dp를 구했으면 모든 간선들의 방향을 바꾼다.

이제는 정점 7을 가리키는 간선 수가 0이므로, 정점 7부터 탐색을 시작한다.
정점 7은 정점 2와 6을 갈 수 있다.
이 때 현재 정점의 dp 값 - 간선의 가중치 == 대상 정점의 dp 라면
해당 정점을 탐색 큐에 넣는다.
정점 7의 dp는 15이고, 정점(7, 6)으로 향하는 간선의 가중치는 5
정점 6의 dp는 10이므로, dp[7] - 5 = 10 이므로, 정점 6을 탐색 큐에 넣는다.
마찬가지로 정점 6의 dp와 간선의 가중치, 정점 2, 3, 4의 dp를 비교한다.
이 경우 정점 2가 탐색 큐에 들어간다.
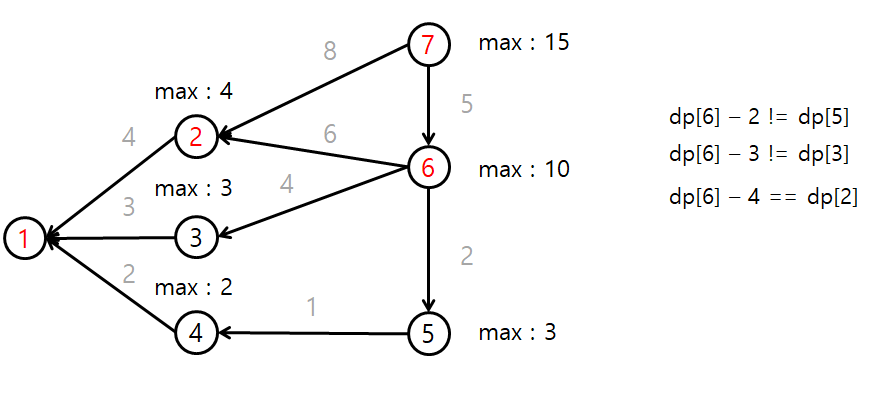
이런식으로 계산을 수행하면
정점 1 -> 2 -> 6-> 7 순으로 가는것이 가장 비용이 큰 루트다.
'알고리즘 > 기법' 카테고리의 다른 글
| 최소 스패닝 트리(MST, Minimum spanning tree) (0) | 2022.01.20 |
|---|---|
| BFS(breadth first search) (0) | 2022.01.17 |
| DFS(depth first search) (0) | 2022.01.15 |
| 유니온 파인드(Union Find) (0) | 2022.01.13 |
| 0-1 BFS (0) | 2021.11.21 |



