업데이트 내역
2023.12.23 노드, 시간 복잡도 및 삽입, 삭제에 알아둘 점 추가
여기서 B-Tree를 테스트해 볼 수 있다.
http://www.cs.usfca.edu/~galles/visualization/BTree.html
B-Tree Visualization
www.cs.usfca.edu
B-Tree 특성
여기서 노드는 RDBMS 기준 최소 단위인 block이라 보면 된다.
- root 노드가 leaf노드가 아닌 경우 최소 2개의 서브트리를 가진다
- 모든 리프 노드들은 같은 레벨을 가져야 함
- node 내부의 키 값들은 오름차순이다.
-> 키 내부에서도 어떤 키의 서브트리를 가야할지 결정해야 한다. - 리프 노드들은 최소 (p/2 -1)개, 최대 (p-1)개의 키를 가져야 함
- 리프가 아닌 노드들은 서브트리 수 - 1개의 키를 가져야 함
-> 키의 대소를 기준으로 서브트리가 생성된다.
p가 뭔데?
4번 항목에서 p는 차수(degree) 란 의미로, 다음 기준으로 결정된다.
- 디스크의 block 크기
- 인덱스를 건 칼럼의 크기
간혹, 다른 포스팅을 보면 p에다 2를 곱한 경우도 있다.
결론부터 말하면 이 부분은 생각하는 방식이 다르기 때문에 교수님 기준으로 따라야 한다.
코드들을 참고하면서 개인적인 생각을 정리하면
- 그냥 p만 씀 -> 결국 분할하는 기준이 block 보다 커지는 경우이기 때문에, 최대 차수를 p로 본다.
- p에 2를 곱함 -> B-Tree의 load factor가 0.5이기 때문에 최대 차수를 2로 나눈 값을 p로 본다.B-Tree의 시간 복잡도
B-Tree의 시간 복잡도
키의 대소를 기준으로 분기를 타기 때문에 logN의 시간 복잡도를 보장한다. (데이터 개수: N)
TMI
B-tree 관련 코드를 보는 중, 키의 탐색을 선형 탐색이나 이분 탐색으로 하는 코드들이 있었다.
엄밀히 말하자면 키의 개수를 M이라 하면
선형 탐색 기준: M * logN
이분 탐색 기준: logM * logN 이 된다.
개인적인 생각으로는 M이 N보다 훨씬 적기 때문에 이 부분은 상수항처럼 무시하는 것 같다.
B-tree의 연산
직접 탐색 : 키 값에 의존한 분기
순차 탐색 : 중위 순회(블록 내에서는 순차 탐색)
삽입, 삭제 : 트리의 균형 유지
-> 분할 : 높이 증가
-> 합병 : 높이 감소
삽입 & 삭제
이 글을 작성한 이후 B-Tree에 구현해 볼 일이 있었고, 찾아본 결과 코드마다 어떻게 분할을 할지 달랐다.
즉, 교바교가 있을 것이기 때문에 이 글에선 이렇게 분할하는구나 정도만 알면 된다.
실제로 B-tree에서 삽입, 삭제 후 결과를 써보란 시험 문제가 나왔기 때문에 블로그 글을 보는 것보단 교재를 참고하는 게 좋다.
삽입
- 항상 리프 노드부터 삽입
- 빈 공간이 없는 경우는(overflow) 분할(split) 적용
-> [p/2]번째의 키 값(중간값)을 부모 노드로 이동
-> 나머지 키값들을 반씩 나눔
다음과 같이 1과 2가 삽입된 상태일 때, 3을 넣는다면
p/2 번째인 1번 키, 즉 2가 부모로 남게 되는데
이렇게 되면, 2는 leaf 노드가 아니게 돼, 2개의 서브 트리를 가져야 한다.

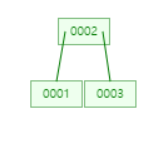
여기서 4를 넣는다면,
4는 2보다 크기 때문에, 2의 오른쪽 서브 트리를 탐색하고,
오른쪽 서브트리엔 빈 공간이 있으니, 그곳에 4를 저장한다.
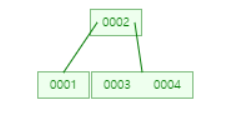
또, 5를 넣는다면
5는 보다 크기 때문에, 2의 오른쪽 서브 트리를 탐색한다.
하지만 이미 오른쪽 서브트리는 공간이 없기 때문에 분할(split)을 사용한다.
{3,4,5} 중에 중간값 4가 부모로 가고, 나머지는 서브 트리에 남아있는다.
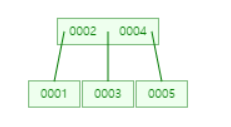
6을 넣는다면, 4를 넣을 때와 동일하게 4의 오른쪽 서브 트리에 저장된다.
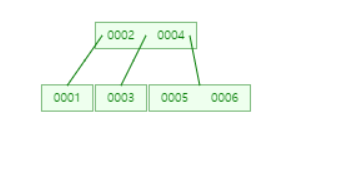
7을 넣는다면,
4의 오른쪽 서브트리엔 공간이 없어, 분할을 사용한다.
{5,6,7}의 중간값인 6이 부모로 올라가지만
부모 노드는 {2,4,6}을 가지게 돼 부모 노드 역시 분할을 사용한다.
4번 키 값이 부모로 올라가고, 2,6은 4의 자식 노드로 남는다.
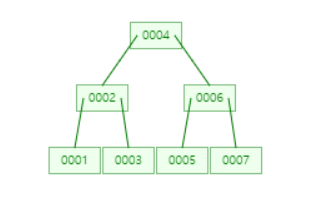
여기까지 B-Tree 삽입에서 일어날 수 있는 모든 경우의 수이다.
삭제
아까의 B-Tree에서 키 값 5를 삭제해본다.

5를 지우면 6의 서브트리는 1개가 남게 되는데,
리프 노드가가 아닌 노드는 2개의 서브 트리를 가져야 하므로
6과 7이 합쳐진다.
하지만, 모든 리프의 depth는 동일해야 하므로,
오른쪽 1, 2, 3에도 병합이 일어난다.
삽입 때 처럼 {1, 2, 3}에서 중간값 2가 부모 노드로 올라가고,
자식 노드{1, 3}은 부모 노드 {2, 4}의 서브트리로 남는다.

'학교 > 데이터베이스' 카테고리의 다른 글
| 12. Transaction Processing (0) | 2020.12.07 |
|---|---|
| 11. B+-tree (0) | 2020.12.06 |
| 9. Single Level ordered Index (0) | 2020.12.06 |
| 8. RAID (0) | 2020.12.06 |
| 7. File (0) | 2020.12.06 |



