업데이트 내역
2023.12.23 B-Tree의 문제점 추가
B-Tree의 문제
시간 복잡도가 균등하지 않다.
노드에도 데이터가 있었기 때문에, logN이라도 상황에 따라선 더 빠를 수도, 늦을 수도 있다.
이러한 문제는 성능 측정 과정에서 모호한 결과를 주게 된다.
이 문제를 해결하기 위해 B+Tree에선 다음과 같이 적용했다.
- 모든 데이터는 리프 노드에 있다.
- 중간 노드는 키값만 저장한다.
인접한 노드 탐색이 어렵다.
WHERE 절에 BETWEEN, IN 같이 범위 조건을 걸게 되면, 인접한 노드라도 부모 노드를 타고 올라가야 한다.
상황에 따라선, 루트 노드까지 올라갈 수도 있기 때문에 무척 비효율적이다.
예를 들면, 다음 트리에서 7 ~ 9를 찾고자 한다면 루트 노드까지 올라가야 한다.
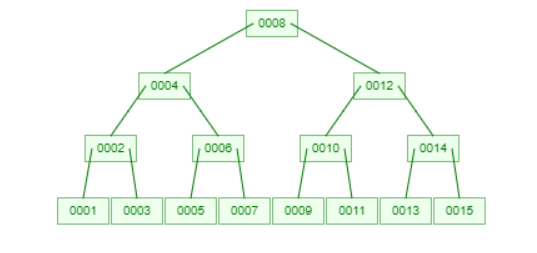
이 문제를 해결하기 위해 리프 노드는 연결리스트 형식으로 관리한다.
인접한 노드라면 O(1) 의 시간 복잡도로 탐색할 수 있다.
B+-tree의 특성
루트의 서브 트리 개수 : [p/2] ~ p
노드의 서브 트리 개수 (루트, 리프 x) : [p/2] ~ p
모든 리프는 동일 레벨
리프가 아닌 노드의 키값 수 : 서브 트리 수 - 1
리프 노드 : 연결 리스트로 관리
사람들마다 p를 어떻게 정하는지, 삽입, 삭제 과정에서 어떻게 분할하는지 갈린다.
따라서, 이 글에선 이렇게 설명하는구나 라고 넘어가고, 교수님 방식을 기준으로 해야 한다.
B-Tree와 마찬가지로 삽입, 삭제 시 합병, 재분배, 분열이 일어남
다만, B-Tree는 중간 값이 부모로 갔지만, B+-tree는 중간값이 리프에도 남아있음
B+-tree의 삽입
루트 노드가 다음과 같을 때, 1과 7을 입력받은 결과
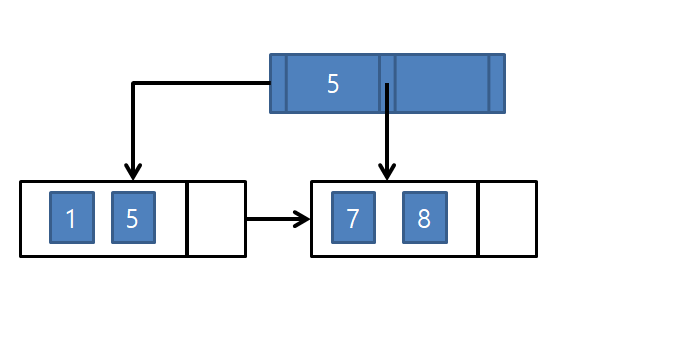
여기서 3을 넣는다고 하면
부모 노드는 {3, 5}가 되고, 3은 5보다 작으니,
왼쪽 서브 트리에 3을 넣어야 한다.
하지만 이미 왼쪽 서브트리엔 5가 있기 때문에 분할(split)을 해줘야 한다.
{1, 3, 5}중 중간값 3은 왼쪽 서브트리에 남고, 오른쪽 서브트리에 5를 넣을 공간이 없기 때문에,
부모 노드 {3, 5}는 가운데 리프 노드를 만들고, 그 자리에 5를 넣는다.
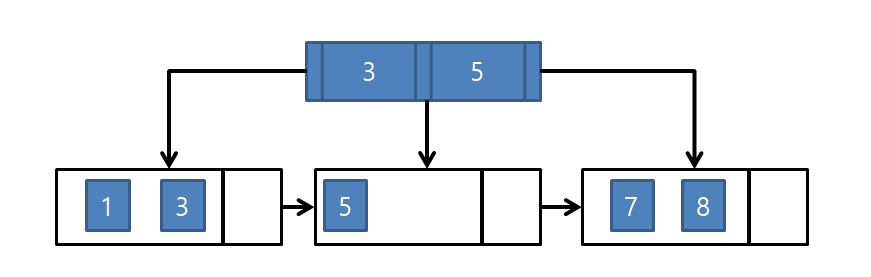
만약 여기서, 12가 들어가게 된다면,
리프 노드 {7, 8, 12}에서 중간값 8이 부모 노드로 올라간다.
하지만, 이미 부모노드엔 여유공간이 없어, 부모 노드에 분열이 일어난다.
부모 노드 {3, 5, 8}에서 중간값 5가 부모 노드로 올라가고,
{3, 8}은 노드 5의 자식 노드가 된다.
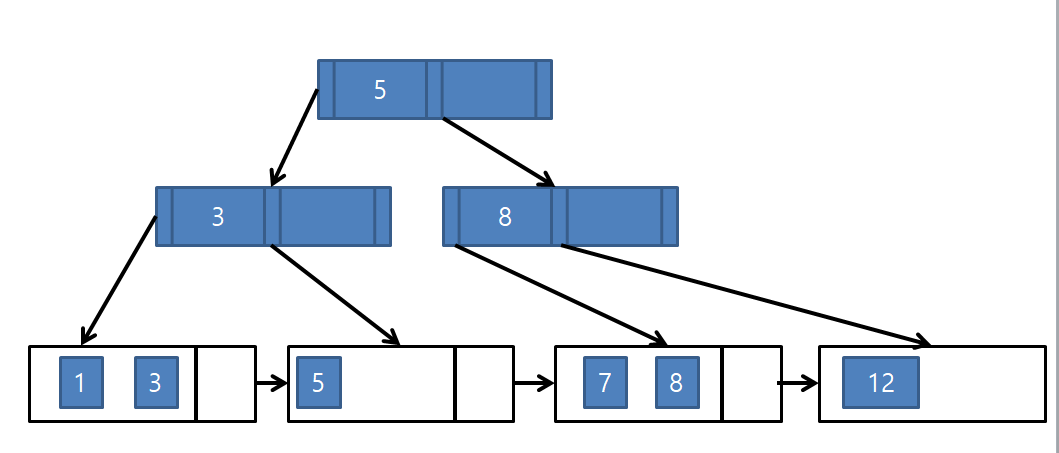
다시 여기에 9를 넣는다면,
B+-tree의 삭제
다음 트리에서 5와,12를 지운다 하자
5를 지워도 underflow가 발생하지 않기 때문에, 교정 작업이 일어나지 않는다.
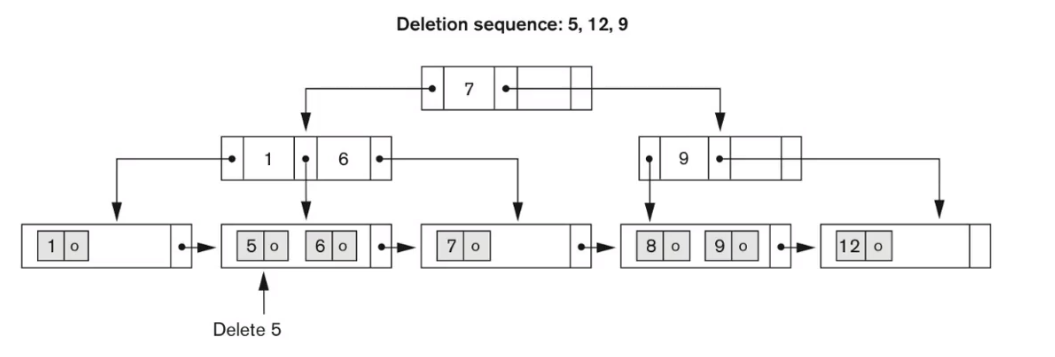
반대로 12를 지우면 9의 가운데 노드에선 underflow가 발생하고,
빈 공간을 채우기 위해, 옆 리프 노드에서 키를 가져올 수 있는지 확인한다.
마침 {8, 9} 가 있으므로, 9를 빈 노드로 옮긴다.
9가 옆 리프 노드로 옮겨갈 때, 부모 노드의 중간값을 넣어주면 된다 (8하고 9 사이 아무거나)
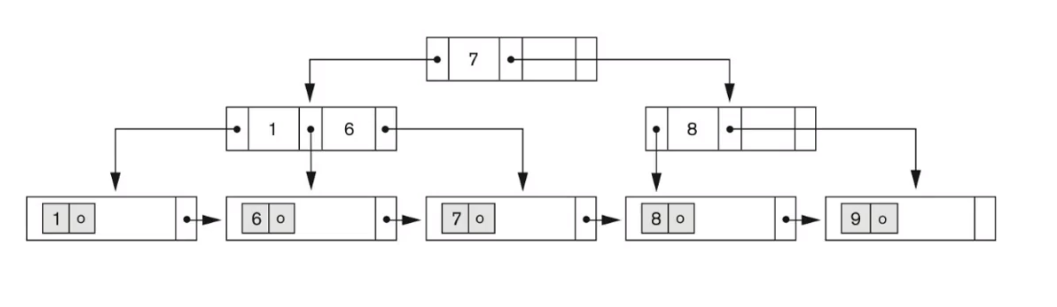
여기에 또 9를 지운다면,
더이상 옆 노드에서 빌려올 키가 없기 때문에
합병이 일어난다.
노드 {1, 6, 7}에서 중간값 6이 부모로 올라가고, 7이 옆 노드의 빈 자리를 채운 다.
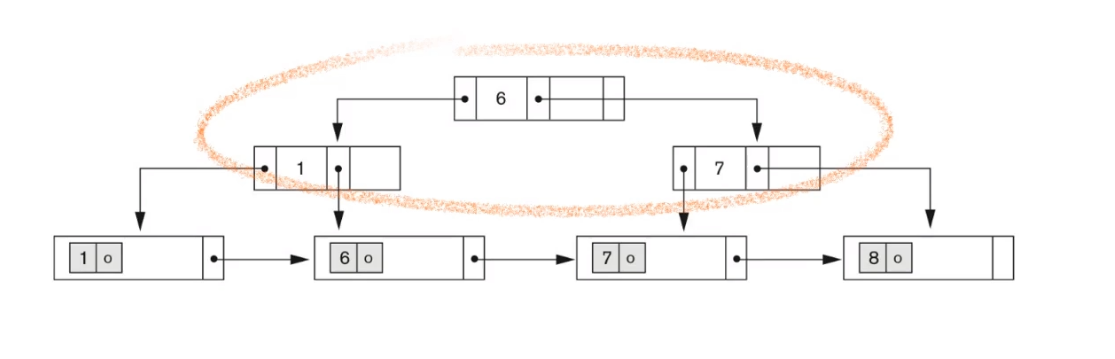
여기에 또 8을 지운다면,
underflow가 발생하고, 더이상 빌려올 키가 없기 때문에
6의 오른쪽 노드를 유지할 수 없어지고,
상위 노드 1과 6이 병합되고,
나머지 리프 노드들이 노드 {1, 6}의 서브 트리가 된다.
'학교 > 데이터베이스' 카테고리의 다른 글
| 13. serialize schedule (0) | 2020.12.07 |
|---|---|
| 12. Transaction Processing (0) | 2020.12.07 |
| 10. B-Tree (0) | 2020.12.06 |
| 9. Single Level ordered Index (0) | 2020.12.06 |
| 8. RAID (0) | 2020.12.06 |



